CATÉGORIES ET FONCTEURS

CATÉGORIES ET FONCTEURS

Introduite en 1945 par Eilenberg et MacLane pour rendre compte de propriétés très générales des structures mathématiques, la théorie des catégories a quelque peu pâti, à ses débuts, de cette généralité qui lui valut auprès des «mathématiciens sérieux» l’appellation de «Abstract Nonsense». Dès 1952 cependant, en définissant les théories de l’homologie comme foncteurs d’une catégorie d’espaces topologiques dans une catégorie algébrique vérifiant certains axiomes et en classifiant ces théories, Eilenberg et Steenrod mettaient en évidence le rôle des catégories comme outil pour la topologie algébrique. Ce rôle était encore accentué par l’axiomatisation par Kan des groupes d’homotopie et par les travaux de Eckmann et Hilton sur la dualité en homotopie. Il devenait essentiel dans les théories algébriques de l’homotopie d’où la topologie disparaissait, sauf en tant qu’exemple.

La possibilité, remarquée par Buchsbaum, d’étendre aux catégories abéliennes les techniques de l’algèbre homologique développées par Cartan et Eilenberg et l’utilisation par Grothendieck de catégories de faisceaux pour la géométrie algébrique furent à l’origine de nombreux travaux sur les catégories abéliennes.

Dans l’étude des structures qui lui avait donné naissance, la théorie des catégories s’est révélée fondamentale. L’introduction par Kan, en 1958, de la notion de foncteurs adjoints fournit un cadre précis pour l’étude des problèmes universels. La définition des théories algébriques comme des petites catégories vérifiant certains axiomes apportait sur l’algèbre une vue nouvelle et féconde.

Notions générales

Catégories

Une catégorie 暈 est constituée par la donnée de:

a ) une classe Ob( 暈) d’objets et une classe Fl( 暈) de flèches ;

b ) deux applications s et b de Fl( 暈) dans Ob( 暈) (pour tout couple (A, B) d’objets, on note Hom(A, B) la classe des flèches f de source s (f ) = A et de but b (f ) = B; si f 捻 Hom(A, B), on écrit f : AB ou A 轢^f B);

c ) une application qui associe à tout couple (g , f ) de flèches composables , i.e. telles que s (g ) = b (f ), une flèche composée , notée g 獵 f ou gf , de source s (f ) et de but b (g ).

Ces données sont soumises aux deux axiomes suivants:

(C. 1) Pour tout objet A, il existe une flèche unité 1^A : AA, telle que 1^A 獵 f = f , et g 獵 1^A = g , pour toute flèche f de but A et toute flèche g de source A;

(C. 2) Si f : AB, g : BC et h : CD, alors (hg ) f = h (gf ).

Les structures mathématiques (ensembles, groupes, espaces topologiques, etc.) sont habituellement munies de morphismes (applications, homomorphismes, applications continues, etc.) et déterminent des catégories ( 劉ns, r, 淪op, etc.) ayant pour objets les ensembles structurés et pour flèches les morphismes; la source et le but d’un morphisme sont ici respectivement les ensembles de départ et d’arrivée du morphisme. On obtient immédiatement des catégories qui ne sont pas du type précédent par des constructions formelles comme les suivantes: si 暈¹ et 暈² sont deux catégories, la catégorie produit 暈¹ 憐 暈² a pour objets les couples formés d’un objet de 暈¹ et un objet de 暈², les flèches de source (A¹, A²) et de but (B¹, B²) étant les couples (f ¹, f ²) où f ¹: A¹B¹ et f ²: A²B². La catégorie duale 暈 d’une catégorie 暈 s’obtient en «renversant le sens» des flèches de 暈.

Beaucoup de notions familières dans le cas des ensembles structurés s’étendent aux catégories abstraites, bien que les objets n’y aient pas de points. C’est ainsi qu’un isomorphisme est une flèche f : AB telle qu’il existe une flèche g : BA vérifiant gf = 1^A et fg = 1^B; un monomorphisme est une flèche f : AB telle que, si h : XA et k : XA vérifient fh = fk , alors h = k. Si (Aⁱ ) (i 捻 I) est une famille d’objets, un objet A muni de flèches p ⁱ : AAⁱ est un produit des Aⁱ si, pour toute famille de flèches (f ⁱ : XAⁱ ), il existe une flèche unique f : XA telle que, pour tout i 捻 I, on ait f ⁱ = p ⁱ f . Un objet A est final , si, pour tout objet X, il existe une flèche unique de source X et de but A. En général, dans les catégories d’ensembles structurés, les monomorphismes s’identifient aux morphismes qui sont des injections, les produits aux produits cartésiens et les objets finaux aux structures à un élément. Dualement, on définit les épimorphismes , les sommes et les objets initiaux d’une catégorie comme monomorphismes, produits et objets finaux de la catégorie duale. Même dans les catégories usuelles, ces définitions ne redonnent pas toujours les notions courantes. Ainsi, dans la catégorie des anneaux commutatifs, la somme de deux anneaux est leur produit tensoriel; dans la catégorie des groupes, la somme est le produit libre. Dans la catégorie des espaces topologiques séparés, une application continue f : AB est un épimorphisme, si f (A) est partout dense dans B.

Foncteurs

Si 暈 et 暈 sont deux catégories, un foncteur F de 暈 dans 暈 associe à tout objet A de 暈 un objet F(A) de 暈 , et à toute flèche f : AB une flèche F(f ) : F(A)F(B), de façon que:

(F. 1) pour tout objet A de 暈,

(F. 2) si (g , f ) est composable dans 暈, F(gf ) = F(g ) F(f ).

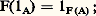Les constructions de structures nouvelles à partir d’anciennes s’étendent aux morphismes et déterminent des foncteurs entre les catégories correspondantes. Par exemple, le n ^e groupe d’homologie singulière Hⁿ (X) (cf. TOPOLOGIE – Topologie algébrique) d’un espace topologique X «est» un foncteur Hⁿ de 淪op dans la catégorie 遼b des groupes abéliens. Les constructions qui changent le sens des flèches, comme l’algèbre C(X) des fonctions continues sur un espace topologique X, donnent naissance à des foncteurs de 暈 dans 暈 , encore appelés foncteurs contravariants de 暈 dans 暈 . Les constructions qui font intervenir plusieurs objets s’interprètent comme des foncteurs définis sur un produit de catégories. Ainsi, le produit tensoriel de deux groupes abéliens détermine un foncteur de 遼b 憐 遼b dans 遼b. Toute catégorie 暈 est munie d’un foncteur Hom de 暈 憐 暈 dans 劉ns qui associe à tout couple (X, Y) d’objets l’ensemble Hom(X, Y) et à tout couple

de flèches, l’application Hom(f , g ) de Hom(X, Y) dans Hom(X , Y ) définie par Hom(f , g ) (u ) = guf (pour u 捻 Hom(X, Y)).

Un foncteur F de 暈 dans 暈 est fidèle si, pour tout couple (A, B) d’objets de 暈, l’application de Hom(A, B) dans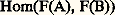

induite par F est une injection. Si cette application est en outre surjective, on dit que F est pleinement fidèle. On dit que F est une équivalence , s’il est pleinement fidèle et si pour tout objet A de 暈 il existe un objet A de 暈 et un isomorphisme

dans 暈 . Les exemples types de foncteurs fidèles sont les foncteurs d’oubli , ainsi nommés parce qu’ils associent à des ensembles structurés des ensembles munis d’une structure moins riche, obtenue en «oubliant» tout ou partie de la structure donnée: l’ensemble sous-jacent à un espace topologique ou le groupe additif sous-jacent à un anneau sont deux tels foncteurs d’oubli de 淪op dans 劉ns ou de 遼n dans 遼b. Les foncteurs pleinement fidèles se rencontrent souvent quand on se limite aux structures vérifiant des axiomes supplémentaires: le foncteur d’inclusion de la catégorie des groupes abéliens dans la catégorie des groupes, par exemple, est pleinement fidèle (on dit que 遼b est une sous-catégorie pleine de r). Enfin, si 暈 est équivalente à 暈 (i.e. s’il existe une équivalence F de 暈 dans 暈 ), alors 暈 est équivalente à 暈 et, en tant que catégories, 暈 et 暈 ont les mêmes propriétés. par exemple, la catégorie des espaces vectoriels de dimension finie sur un corps K est équivalente à la sous-catégorie pleine ayant pour objets les Kⁿ (n 捻 N); ou encore, en utilisant la dualité de Pontriaguine, la catégorie des groupes compacts abéliens est équivalente à la catégorie 遼b.

Transformations naturelles

Soit 暈 et 暈 deux catégories, et F et G deux foncteurs de 暈 dans 暈 ; on appelle transformation naturelle de F dans G, et on note 﨏 : FG, une application 﨏 de Ob( 暈) dans Fl( 暈 ) vérifiant:

(N.1) pour tout objet A de 暈

(N.2) pour toute flèche f : AB de 暈, on a: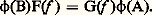

Tous les isomorphismes ou homomorphismes «canoniques», si fréquents en mathématiques, sont des transformations naturelles: c’est précisément pour formaliser cette «naturalité» que les catégories furent créées.

Si H est un troisième foncteur de 暈 dans 暈 et 祥 : GH une transformation naturelle, en associant à tout objet A de 暈 la flèche 祥(A) 﨏(A) : F(A)H(A) on obtient la transformation naturelle 祥﨏 composée de 祥 et 﨏. D’où la catégorie 杻onct( 暈, 暈 ) ayant pour objets les foncteurs de 暈 dans 暈 et pour flèches les transformations naturelles. Les catégories de foncteurs jouent un rôle essentiel; en effet, beaucoup de propriétés des foncteurs ou transformations naturelles s’expriment simplement en tant que propriétés d’objets ou de flèches d’une catégorie de foncteurs; par exemple, une transformation naturelle 﨏 : FG est une équivalence naturelle (i.e. pour tout objet A de 暈, 﨏(A) est un isomorphisme), si 﨏 est un isomorphisme dans 杻onct( 暈, 暈 ). En outre, les catégories les plus importantes (faisceaux, ensembles simpliciaux, catégories algébriques, etc.) apparaissent comme sous-catégories, en général pleines, de catégories de la forme 杻onct( 暈, 劉ns) ou 杻onct( 暈, 遼b) où 暈 est une petite catégorie (i.e. telle que Ob( 暈) et Fl( 暈) sont des ensembles). Enfin, si 暈, 暈 et 阮 sont des catégories et F un foncteur de 暈 憐 暈 dans 阮, tout objet A de 暈 détermine un foncteur F(A, -) de 暈 dans 阮 qui associe à tout objet A de 暈 l’objet F(A, -) (A ) = F(A, A ) de 阮 et à toute flèche f : A B de 暈 la flèche

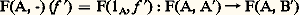de 阮. De même, toute flèche f : AB de 暈 détermine une transformation naturelle F(f , -) : F(A, -)F(B, -), c’est-à-dire que F détermine un foncteur ¹ de 暈 dans 杻onct( 暈 , 阮). Cette correspondance permet d’identifier les catégories 杻onct( 暈 憐 暈 , 阮) et 杻onct( 暈, 杻onct( 暈 , 阮)) et de remplacer les foncteurs à deux variables par des foncteurs à une variable à valeurs dans une catégorie de foncteurs. En changeant les rôles de 暈 et 暈 , on identifie de même 杻onct( 暈 憐 暈 , 阮) et 杻onct( 暈 , 杻onct( 暈, 阮).

Propriétés des foncteurs

Soit 暈 une catégorie; le foncteur Hom de 暈 憐 暈 dans 劉ns détermine un foncteur H⁰ de 暈 dans 杻onct( 暈, 劉ns) = 暈 qui associe à tout objet A le foncteur:

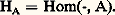Si F est un foncteur de 暈 dans 劉ns, toute transformation naturelle 﨏 : H^AF détermine un élément 靖( 﨏) = 﨏(A) (1^A) de F(A). Inversement, tout élément x de F(A) détermine une transformation naturelle 精(x ) : H^AF qui associe à tout objet X l’application:

définie par: 精(x ) (X) (f ) = F(f ) (x ), pour f 捻 Hom(X, A). Les applications

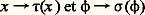sont des bijections inverses l’une de l’autre qui permettent d’identifier l’ensemble Hom(H^A, F) des transformations naturelles de H^A dans F et l’ensemble F(A). En particulier, si on prend pour F un foncteur H^B, l’application de

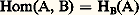dans Hom(H^A, H^B), induite par H, est bijective, c’est-à-dire que H est pleinement fidèle, et identifie 暈 à une sous-catégorie pleine de 杻onct( 暈, 劉ns.).

Foncteurs représentables

Ce résultat, dû à Yoneda, suggère les deux questions suivantes:

– Peut-on remplacer 暈 par une catégorie plus petite? Des réponses affirmatives sont données par exemple dans le cas des catégories algébriques.

– Peut-on caractériser l’«image» de H, c’est-à-dire reconnaître quand un foncteur F de 暈 dans 劉ns est de la forme H^A, ou même représentable , c’est-à-dire isomorphe à un foncteur H^A? Un exemple important historiquement a été la construction des espaces d’Eilenberg-MacLane pour représenter les foncteurs de cohomologie.

Notons que si F est représentable, le représentant A est déterminé à un isomorphisme unique près. Dualement, on définit un foncteur pleinement fidèle H de 暈 dans 杻onct( 暈, 劉ns), qui associe à tout objet A le foncteur H^A = Hom(A,-). Un foncteur F de 暈 dans 劉ns est représentable, s’il est isomorphe à un H^A. La notion de foncteur représentable est liée à la notion suivante de problème universel . Soit U : 暈 暈 un foncteur et A un objet de 暈 . On se propose de trouver un objet A de 暈 et une flèche

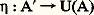tels que, pour tout objet X de 暈 et toute flèche f : A U(X) de 暈 , il existe une flèche unique f : AX de 暈 telle que f = U(f ) 兀. On dit alors que A est libre sur A (relativement à U) et que 兀 est une flèche de liberté. Au couple (A , U), on associe le foncteur 淋 de 暈 dans 劉ns défini par 淋(X) = Hom(A ,U(X)). La donnée de 兀 捻 淋(A) détermine une transformation naturelle 靖( 兀) : H^A淋, qui est un isomorphisme si et seulement si 兀 est une flèche de liberté. Ainsi le problème d’existence d’un objet libre sur A est équivalent à celui de reconnaître si le foncteur 淋 est représentable.

Par exemple, si U : r 劉ns est le foncteur d’oubli et si X est un ensemble, le groupe libre engendré par X est «libre» au sens précédent, et l’inclusion canonique de X comme ensemble des générateurs est une flèche de liberté (on peut dans cet exemple remplacer la catégorie des groupes par n’importe quelle catégorie algébrique).

Limites

Les produits, les sommes et plus généralement les limites sont des solutions de problèmes universels: soit 暈 une catégorie et 琉 une petite catégorie. Le foncteur projection de 暈 憐 琉 dans 暈 détermine un foncteur U de 暈 dans 杻onct( 琉, 暈); si F est un objet de 杻onct( 琉, 暈), une solution du problème universel posé par U et F s’appelle une limite inductive du foncteur F. En explicitant, on voit qu’une telle limite est constituée par un objet de 暈, noté lim 轢F, muni pour tout objet I de 琉 d’une flèche q (I): F(I)lim 轢F, tel que:

(1) pour toute flèche 見: IJ dans 琉, on a q (I) = q (J) F( 見);

(2) si (f ^I : F(I)X) (I 捻 Ob( 琉)) est une famille de flèches telles que f ^I = f ^JF( 見); alors pour toute 見 : IJ, il existe une flèche unique f : lim 轢FX telle que, pour tout I 捻 Ob( 琉), on ait f ^I = f 獵 q (I).

La limite projective se définit de même comme un objet lim 良F, muni de flèches s (I): lim 良(F)F(I) vérifiant les propriétés duales de (1) et (2). Si 琉 est une catégorie discrète (i.e. dont toutes les flèches sont des unités), les limites projectives et inductives s’identifient aux produits et aux sommes des familles d’objets indexées par Ob( 琉); si 琉 est la catégorie représentée par: 1^I I 轢轢 見廓 J 1^J, un foncteur F de 琉 dans une catégorie 暈 s’identifie à un couple de flèches A 轢轢fg B et la limite inductive de F est appelée conoyau de (f , g ); c’est un objet Coker(f , g ) de 暈, muni d’une flèche C : BCoker(f , g ) telle que:

(1) cf = cg ;

(2) si h : BX est une flèche telle que hf = hg , il existe une flèche

unique telle que h = h c.

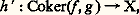La limite projective de F est le noyau Ker(f , g ) de (f , g ), il est muni d’une flèche k : Ker(f , g )A vérifiant les conditions duales de (1) et (2).

Une catégorie 暈 est complète à gauche , si tout foncteur d’une petite catégorie 琉 à valeur dans 暈 a une limite projective. Il suffit pour cela que toute famille d’objets de 暈 ait un produit et que tout couple de flèches A 轢轢 B ait un noyau. Dualement, on a la notion de catégorie complète à droite. Les catégories usuelles d’ensembles structurés sont complètes (à droite et à gauche).

Foncteurs adjoints

Soit U : 暈 阮 et F : 阮 暈 des foncteurs; on dit que F est adjoint à gauche de U (et U adjoint à droite de F), si les deux foncteurs de 阮 憐 暈 dans 劉ns qui associent à tout couple (D, C) d’objets les ensembles Hom(F(D),C) et Hom(D, U(C)) sont isomorphes. Chacun des foncteurs U et F détermine l’autre à isomorphisme près. Pour tout objet D de 阮, l’objet F(D) est libre sur D, relativement à U; inversement, si, pour tout objet de 阮, il existe un objet libre, U a un adjoint à gauche. La recherche de l’adjoint à gauche d’un foncteur U revient donc à la solution d’une classe de problèmes universels. Les méthodes générales reposent sur les remarques suivantes: si U a un adjoint à gauche, il commute avec les limites projectives , c’est-à-dire que, si (A, p (I)) est la limite projective d’un foncteur 淋 : 琉 暈, alors (U(A), U(p (I))) est limite projective du foncteur composé

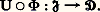Cette propriété est «presque» caractéristique: si 暈 est complète à gauche, et si U n’est pas «trop grand», il suffit qu’il commute avec les limites projectives pour qu’il ait un adjoint à gauche.

Catégories abéliennes

Soit 暈 une catégorie; un objet O de 暈 est nul s’il est à la fois initial et final. Si 暈 a un objet nul, pour tout couple (A, B) d’objets Hom(A, B) a une flèche nulle , notée ^AB ou O, qui est la composée des flèches AO et OB. Le noyau Ker(f ) d’une flèche f : AB est le noyau du couple (f , O), le conoyau de (f , O) est appelé conoyau de f et noté Coker(f ).

Les axiomes suivants pour qu’une catégorie soit abélienne sont dus à Freyd:

(A.0) 暈 a un objet nul;

(A.1) tout couple d’objets a une somme et un produit;

(A.2) toute flèche a un noyau et un conoyau;

(A.3) tout monomorphisme est un noyau et tout épimorphisme un conoyau.

On montre alors que pour tout couple (A, B) d’objets, Hom(A, B) a une structure canonique de groupe abélien et que les applications de

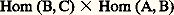dans Hom(A, C) induites par la composition des flèches sont bilinéaires. L’image Im(f ) d’une flèche f : AB est définie par Im(f ) = Ker(Coker(f )). Une suite A 轢f B 轢g C est exacte en B, si

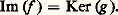Un foncteur F d’une catégorie abélienne 暈 dans une catégorie abélienne 暈 est exact à gauche , s’il transforme tout noyau en un noyau. Il en résulte qu’il est additif , c’est-à-dire que, pour tout couple (A, B) d’objets, l’application de Hom(A, B) dans Hom(F(A), F(B)) est un homomorphisme de groupes abéliens. Dualement, F est exact à droite , s’il transforme conoyaux en conoyaux, et F est exact s’il est exact à droite et à gauche. Il transforme alors toute suite exacte en suite exacte. Une sous-catégorie exacte 暈 d’une catégorie abélienne 暈 est une sous-catégorie abélienne telle que le foncteur d’inclusion est exact.

Les catégories abéliennes types sont les catégories 紐od^A, de modules à gauche sur un anneau A: Mitchell a montré que toute petite catégorie abélienne est une sous-catégorie pleine et exacte d’une catégorie de modules. Il en résulte que toutes les propriétés relatives aux suites exactes, vraies dans les catégories de modules, sont vraies dans toute catégorie abélienne. Les techniques de l’algèbre homologique s’étendent presque sans changement aux catégories abéliennes en utilisant les définitions suivantes: un objet P d’une catégorie 暈 est projectif , si le foncteur Hom(P,-) de 暈 dans la catégorie 遼b des groupes abéliens est exact; on dit que 暈 a assez de projectifs si, pour tout objet A de 暈, il existe un épimorphisme f : PA où P est projectif. Dualement, on a la notion d’objet injectif et de catégorie ayant assez d’injectifs. On peut alors définir, comme dans le cas des modules, les foncteurs dérivés d’un foncteur additif, qui jouent un rôle important dans la théorie des faisceaux par exemple, si essentielle dans la théorie des variétés différentiables ou des fonctions analytiques de plusieurs variables complexes.

Encyclopédie Universelle. 2012.